Exercice 1 8 points
On note i le nombre complexe de module 1 et d'argument π 2 \dfrac{\pi}{2} 2 π
1. On considère le nombre complexe
z 1 = 2 e i π 4 z_1 = \sqrt{2}\text{e}^{\text{i}\frac{\pi}{4}} z 1 = 2 e i 4 π
1. a) Écrire z 1 z_1 z 1
On sait que
cos π 4 = sin π 4 = 2 2 \cos \frac{\pi}{4} = \sin \frac{\pi}{4} = \frac{\sqrt{2}}{2} cos 4 π = sin 4 π = 2 2
z 1 = 2 e i π 4 = 2 ( cos π 4 + i sin π 4 ) = 2 ( 2 2 + i 2 2 ) = 1 + i z_1 = \sqrt{2}\text{e}^{\text{i}\frac{\pi}{4}} = \sqrt{2}\left(\cos \frac{\pi}{4} + \text{i} \sin \frac{\pi}{4}\right) = \sqrt{2}\left(\frac{\sqrt{2}}{2} + \text{i}\frac{\sqrt{2}}{2} \right) = 1 + \text{i} z 1 = 2 e i 4 π = 2 ( cos 4 π + i sin 4 π ) = 2 ( 2 2 + i 2 2 ) = 1 + i
1. b) Vérifier que z 1 z_1 z 1 ( 2 + i ) z = 1 + 3 i (2 + \text{i})z = 1 + 3\text{i} ( 2 + i ) z = 1 + 3 i
∙ \bullet~~ ∙
( 2 + i ) ( 1 + i ) = 1 + 3 i ⟺ 2 + 2 i + i − 1 = 1 + 3 i (2 + \text{i})(1 + \text{i}) = 1 + 3\text{i} \iff 2 + 2\text{i} + \text{i} - 1 = 1 + 3\text{i} ( 2 + i ) ( 1 + i ) = 1 + 3 i ⟺ 2 + 2 i + i − 1 = 1 + 3 i
∙ \bullet~~ ∙
( 2 + i ) z = 1 + 3 i ⟺ z = 1 + 3 i ( 2 + i ) = ( 1 + 3 i ) ( 2 − i ) ( 2 + i ) ( 2 − i ) = 2 + 3 + 6 i − i 4 + 1 = 5 + 5 i 5 = 1 + i (2 + \text{i})z = 1 + 3\text{i} \iff z = \dfrac{1 + 3\text{i}}{(2 + \text{i})} = \dfrac{(1 + 3\text{i})(2 - \text{i})}{(2 + \text{i})(2 - \text{i})} = \dfrac{2 + 3 + 6\text{i} - \text{i}}{4 + 1} = \dfrac{5 + 5\text{i}}{5} = 1 + \text{i} ( 2 + i ) z = 1 + 3 i ⟺ z = ( 2 + i ) 1 + 3 i = ( 2 + i ) ( 2 − i ) ( 1 + 3 i ) ( 2 − i ) = 4 + 1 2 + 3 + 6 i − i = 5 5 + 5 i = 1 + i
2. Écrire le nombre complexe z 2 = − 1 + i 3 z_2 = - 1 + \text{i}\sqrt{3} z 2 = − 1 + i 3
On calcule d'abord le module de z 2 z_2 z 2
∣ z 2 ∣ 2 = 1 + 3 = 4 = 2 2 \left|z_2\right|^2 = 1 + 3 = 4 = 2^2 ∣ z 2 ∣ 2 = 1 + 3 = 4 = 2 2 ∣ z 2 ∣ = 2 \left|z_2\right| = 2 ∣ z 2 ∣ = 2
On factorise ce module dans l'écriture de z 2 z_2 z 2
z 2 = 2 ( − 1 2 + i 3 2 ) z_2 = 2\left(- \dfrac{1}{2} + \text{i}\dfrac{\sqrt{3}}{2} \right) z 2 = 2 ( − 2 1 + i 2 3 )
On reconnait − 1 2 = cos 2 π 3 - \dfrac{1}{2} = \cos \frac{2\pi}{3} − 2 1 = cos 3 2 π 3 2 = sin 2 π 3 \dfrac{\sqrt{3}}{2} = \sin \frac{2\pi}{3} 2 3 = sin 3 2 π
z 2 = 2 ( cos 2 π 3 + i sin 2 π 3 ) = 2 e i 2 π 3 z_2 = 2\left(\cos \frac{2\pi}{3} + \text{i}\sin \frac{2\pi}{3}\right) = 2\text{e}^{\text{i}\frac{2\pi}{3}} z 2 = 2 ( cos 3 2 π + i sin 3 2 π ) = 2 e i 3 2 π
3. On considère z 3 z_3 z 3 7 π 6 \dfrac{7\pi}{6} 6 7 π
Vérifier que z 3 = z 1 2 × z 2 z_3 = z_1^2 \times z_2 z 3 = z 1 2 × z 2
On a donc z 3 = 4 e 7 π 6 z_3 = 4\text{e}^{\frac{7\pi}{6}} z 3 = 4 e 6 7 π
D'autre part
z 1 2 × z 2 = ( 2 e i π 4 ) 2 × 2 e i 2 π 3 = 2 e i π 2 × 2 e 2 π 3 = 4 e i ( π 2 + 2 π 3 ) = 4 e i ( 3 π 6 + 4 π 6 ) = 4 e i 7 π 6 z_1^2 \times z_2 = \left(\sqrt{2}\text{e}^{\text{i}\frac{\pi}{4}}\right)^2\times 2\text{e}^{\text{i}\frac{2\pi}{3}} = 2\text{e}^{\text{i}\frac{\pi}{2}}\times 2\text{e}^{\frac{2\pi}{3}} = 4 \text{e}^{\text{i}\left(\frac{\pi}{2} + \frac{2\pi}{3}\right)} = 4\text{e}{\text{i}\left(\frac{3\pi}{6} + \frac{4\pi}{6}\right)} = 4\text{e}^{\text{i}\frac{7\pi}{6}} z 1 2 × z 2 = ( 2 e i 4 π ) 2 × 2 e i 3 2 π = 2 e i 2 π × 2 e 3 2 π = 4 e i ( 2 π + 3 2 π ) = 4 e i ( 6 3 π + 6 4 π ) = 4 e i 6 7 π
On a donc z 3 = z 1 2 × z 2 z_3 = z_1^2 \times z_2 z 3 = z 1 2 × z 2
4. Le plan complexe est muni d'un repère orthonormé
( O ; u → , v → ) \left(\text{O};~\overrightarrow{u},~\overrightarrow{v}\right) ( O ; u , v )
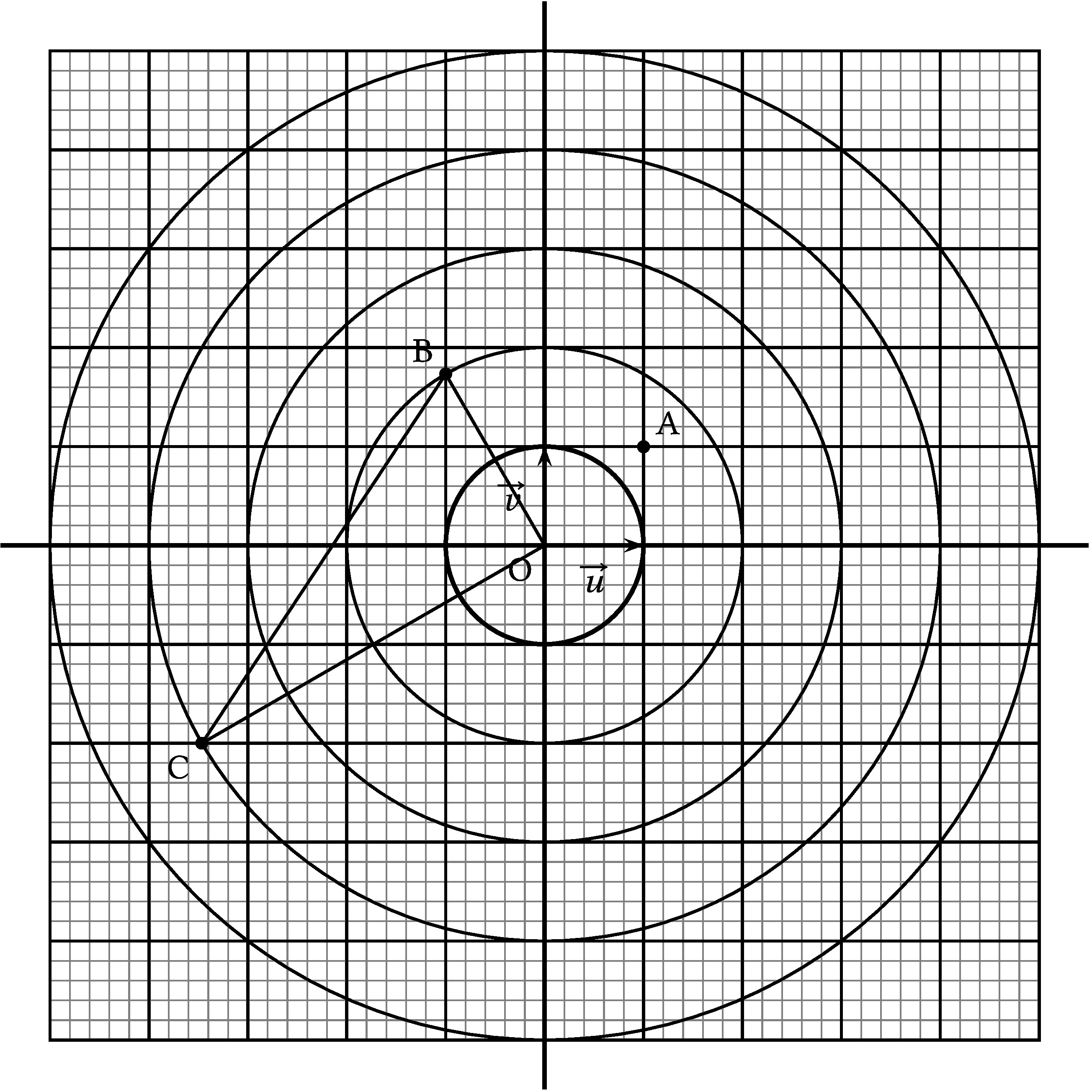
On considère les trois points A, B et C d'affixes respectives
z A = 1 + i z_{\text{A}} = 1 + \text{i} z A = 1 + i z B = − 1 + i 3 z_{\text{B}} = - 1 + \text{i}\sqrt{3} z B = − 1 + i 3
z C = − 2 3 − 2 i z_{\text{C}} = -2\sqrt{3} - 2\text{i} z C = − 2 3 − 2 i
4. a) Placer les points A, B et C dans le plan complexe ci-dessous. On
laissera les éventuels traits de construction apparents.
4. b) Démontrer que le triangle OBC est rectangle en O.
On a OB → ( − 1 3 ) \overrightarrow{\text{OB}}
\begin{pmatrix}-1\\\sqrt{3}\end{pmatrix}
OB ( − 1 3 ) OC → ( − 2 3 − 2 ) \overrightarrow{\text{OC}}
\begin{pmatrix}-2\sqrt{3}\\- 2\end{pmatrix}
OC ( − 2 3 − 2 )
Calculons le produit scalaire
OB → ⋅ OC → = − 1 × ( − 2 3 ) + 3 × ( − 2 ) = 2 3 − 2 3 = 0 \overrightarrow{\text{OB}} \cdot \overrightarrow{\text{OC}} = - 1 \times (-2\sqrt{3}) + \sqrt{3} \times (- 2) = 2\sqrt{3} - 2\sqrt{3} = 0 OB ⋅ OC = − 1 × ( − 2 3 ) + 3 × ( − 2 ) = 2 3 − 2 3 = 0 OB → \overrightarrow{\text{OB}} OB OC → \overrightarrow{\text{OC}} OC
Exercice 2 2 points
On note u u u u = 2 + 2 i u=2+2i u = 2 + 2 i u ‾ \overline{u} u
Démontrer que: u 2020 + u ‾ 2020 = − 2 3031 u^{2020}+\overline{u}^{2020}=-2^{3031} u 2 0 2 0 + u 2 0 2 0 = − 2 3 0 3 1
∣ u ∣ = . . . = 2 2 |u|=...=2\sqrt{2} ∣ u ∣ = . . . = 2 2 arg ( u ) = π 4 \arg(u)=\frac{\pi}{4} arg ( u ) = 4 π ∣ u 2020 ∣ = ∣ u ∣ 2020 = ( 2 2 ) 2020 = 2 2020 × 2 2020 = 2 2020 × 2 1010 = 2 3030 |u^{2020}|=|u|^{2020}=(2\sqrt{2})^{2020}=2^{2020}\times\sqrt{2}^{2020}=2^{2020}\times2^{1010}=2^{3030} ∣ u 2 0 2 0 ∣ = ∣ u ∣ 2 0 2 0 = ( 2 2 ) 2 0 2 0 = 2 2 0 2 0 × 2 2 0 2 0 = 2 2 0 2 0 × 2 1 0 1 0 = 2 3 0 3 0 arg ( u 2020 ) = 2020 × arg ( u ) = 2020 × π 4 = 505 π ≡ π [ 2 π ] \arg\left(u^{2020}\right)=2020\times\arg(u)=2020\times\frac{\pi}{4}=505\pi \equiv \pi [2\pi] arg ( u 2 0 2 0 ) = 2 0 2 0 × arg ( u ) = 2 0 2 0 × 4 π = 5 0 5 π ≡ π [ 2 π ] u u u 2 3030 2^{3030} 2 3 0 3 0 π \pi π u = − 2 3030 u=-2^{3030} u = − 2 3 0 3 0 u ‾ 2020 = u 2020 ‾ = − 2 3030 \overline{u}^{2020}=\overline{u^{2020}}=-2^{3030} u 2 0 2 0 = u 2 0 2 0 = − 2 3 0 3 0 u 2020 + u ˉ 2020 = 2 × ( − 2 3030 ) = − 2 3031 u^{2020}+\bar{u}^{2020} = 2\times\left(-2^{3030}\right)= -2^{3031} u 2 0 2 0 + u ˉ 2 0 2 0 = 2 × ( − 2 3 0 3 0 ) = − 2 3 0 3 1
Dernière mise à jour: 5/4/2021, 4:14:12 PM